加密算法
0x00 前言
本文用于记录一些常见的加密算法,以及其识别特征。
0x01 算法
1.1 md5
1.简介
MD5(Message Digest Algorithm 5,消息摘要算法 5)是一种广泛使用的哈希函数,能够将任意长度的输入数据(消息)转换为固定长度的输出(128位,即16字节)的哈希值(又称为消息摘要)。它由 Ronald Rivest 在 1991 年设计,是继 MD2、MD4 之后的又一版本。
其具有以下特点:
- 固定输出长度:128位,16字节
- 单向性:无法通过hash推出原始输入数据
- 抗碰撞性:理论上应该无法找出两个不同输入产出相同输出,但是已经被验证存在漏洞
2.算法实现
- 消息填充
- 首先填充消息至长度为448 mod 512(这里至少填充1位,至多填充512位,因为至少填充一次)。填充方法为先填充一个1,后面用0填充。
- 添加长度
- 在上一步的结果之后填充64位的消息长度(长度单位为比特,bit)。如果消息填充前的长度大于2^64那么记录长度的低64位。填充之后消息长度正好为448+64=512的整数倍。
- 初始化变量
- 定义四个32位的寄存器变量A=0x67452301,B=0xEFCDAB89,C=0x89ABCDEF,D=0x01234567。在内存中其低字节在前,所以是ABCD=01 23 45 ..... 23 45 67。
- 数据处理
- 对每个数据块进行 64 轮运算,依次使用四种非线性函数(F、G、H、I),并使用不同的常量和数据块。每轮运算都会对 (A, B, C, D) 进行更新。
- 输出摘要
- 将 (A, B, C, D) 的最终值连接起来,形成 128 位的哈希值。
3.代码实现
#include <stdio.h>
#include <string.h>
#include <stdint.h>
// 定义常量
#define F(x, y, z) ((x & y) | (~x & z))
#define G(x, y, z) ((x & z) | (y & ~z))
#define H(x, y, z) (x ^ y ^ z)
#define I(x, y, z) (y ^ (x | ~z))
#define LEFTROTATE(x, c) ((x << c) | (x >> (32 - c)))
// 初始化向量
uint32_t A = 0x67452301;
uint32_t B = 0xEFCDAB89;
uint32_t C = 0x98BADCFE;
uint32_t D = 0x10325476;
// 每轮循环的左移位数
const uint32_t s[64] = {
7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22,
5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20,
4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23,
6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21 };
// T[i] 是MD5的常量表,定义了 2^32 * abs(sin(i+1)) 的结果 用来消除线性
const uint32_t K[64] = {
0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee,
0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be,
0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa,
0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed,
0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c,
0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05,
0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039,
0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 };
// MD5核心计算函数
void md5_transform(uint32_t* state, const uint8_t block[64]) {
uint32_t a = state[0], b = state[1], c = state[2], d = state[3], f, g, temp;
uint32_t M[16];
// 将块数据转为16个32位整数
for (int i = 0; i < 16; ++i) {
M[i] = (block[i * 4]) | (block[i * 4 + 1] << 8) |
(block[i * 4 + 2] << 16) | (block[i * 4 + 3] << 24);
}
// 64轮循环
for (int i = 0; i < 64; ++i) {
if (i < 16) {
f = F(b, c, d);
g = i;
}
else if (i < 32) {
f = G(b, c, d);
g = (5 * i + 1) % 16;
}
else if (i < 48) {
f = H(b, c, d);
g = (3 * i + 5) % 16;
}
else {
f = I(b, c, d);
g = (7 * i) % 16;
}
temp = d;
d = c;
c = b;
b = b + LEFTROTATE((a + f + K[i] + M[g]), s[i]);
a = temp;
}
// 更新状态
state[0] += a;
state[1] += b;
state[2] += c;
state[3] += d;
}
// MD5主函数
void md5(const uint8_t* msg, size_t len, uint8_t digest[16]) {
uint32_t state[4] = { A, B, C, D };
uint8_t block[64];
size_t i;
// 处理每个64字节块
for (i = 0; i + 64 <= len; i += 64) {
memcpy(block, msg + i, 64);
md5_transform(state, block);
}
// 填充
size_t rem = len - i;
memcpy(block, msg + i, rem);
block[rem++] = 0x80;
if (rem > 56) {
memset(block + rem, 0, 64 - rem);
md5_transform(state, block);
rem = 0;
}
memset(block + rem, 0, 56 - rem);
uint64_t bits_len = len * 8;
memcpy(block + 56, &bits_len, 8);
md5_transform(state, block);
// 输出结果
for (i = 0; i < 4; ++i) {
digest[i * 4] = state[i] & 0xff;
digest[i * 4 + 1] = (state[i] >> 8) & 0xff;
digest[i * 4 + 2] = (state[i] >> 16) & 0xff;
digest[i * 4 + 3] = (state[i] >> 24) & 0xff;
}
}
// 测试程序
int main() {
const char* message = "Hello, MD5!";
uint8_t digest[16];
md5((const uint8_t*)message, strlen(message), digest);
printf("MD5(\"%s\") = ", message);
for (int i = 0; i < 16; ++i) {
printf("%02x", digest[i]);
}
printf("\n");
return 0;
}
4.逆向
特点1:
四个初始化向量
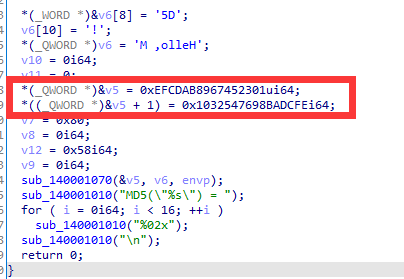
特点2:
首先是数据分组,随后是循环处理数据,最后更新输出
5. 魔改
1.修改MD5的4个初始参数。
2.修改64轮运算使用的常熟数组原始算法为2^32 * abs(sin(i+1))。
3.修改四个非线性变化函数FGHI。
1.2 SHA
1.简介
SHA(Secure Hash Algorithm)是一组密码散列函数,由美国国家安全局(NSA)设计,用于生成固定长度的散列值。SHA算法广泛应用于数据完整性验证、数字签名等安全领域。SHA算法有很多版本SHA-0(散列长度160位),SHA-1(散列长度160位),SHA-2(散列长度224,256,384,512位),SHA-3(散列长度224,256,384,512位)。
以下以SHA-2的变种SHA-256为例。
2.算法实现
- 消息填充
- 首先填充消息至长度为448 mod 512(这里至少填充1位,至多填充512位,因为至少填充一次)。填充方法为先填充一个1,后面用0填充。
- 添加长度
- 在上一步的结果之后填充64位的消息长度(长度单位为比特,bit)。如果消息填充前的长度大于2^64那么记录长度的低64位。填充之后消息长度正好为448+64=512的整数倍。
- 初始化变量
- SHA-256 使用8个32位的初始常量(称为初始散列值):
- H0 = 0x6a09e667
H1 = 0xbb67ae85
H2 = 0x3c6ef372
H3 = 0xa54ff53a
H4 = 0x510e527f
H5 = 0x9b05688c
H6 = 0x1f83d9ab
H7 = 0x5be0cd19
- 数据处理
- 对每个512位的消息块,进行以下操作:
- 扩展消息:
- 将512位的消息块扩展为64个32位的字(W₀到W₆₃)。
- 前16个字直接取自消息块,其余字通过以下公式生成:
- W_t = σ₁(W_{t-2}) + W_{t-7} + σ₀(W_{t-15}) + W_{t-16}
- 压缩函数:
- 使用64轮的压缩函数更新散列值。
- 每轮使用一个32位的常量(Kₜ)和一个扩展字(Wₜ)。
- 压缩函数的核心操作包括:
- 位运算:与(AND)、或(OR)、非(NOT)、异或(XOR)。
- 模加法:对2³²取模的加法。
- 循环移位:将数据的位循环移动一定位置。
- 扩展消息:
- 更新散列值
- 每处理完一个消息块后,更新初始散列值(H₀到H₇)。
- 最终散列值是所有消息块处理完成后,H₀到H₇的连接结果。
- 输出
- 将最终的H₀到H₇连接起来,生成一个256位的散列值。
3.代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdint.h>
// SHA-256常量
#define SHA256_BLOCK_SIZE 64 // 512位块大小(字节)
#define SHA256_DIGEST_SIZE 32 // 256位散列值大小(字节)
// 初始散列值
static const uint32_t K[64] = {
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
};
// 循环右移
#define ROTR(x, n) (((x) >> (n)) | ((x) << (32 - (n))))
// 选择函数
#define Ch(x, y, z) (((x) & (y)) ^ (~(x) & (z)))
// 多数函数
#define Maj(x, y, z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z)))
// Σ0函数
#define Sigma0(x) (ROTR(x, 2) ^ ROTR(x, 13) ^ ROTR(x, 22))
// Σ1函数
#define Sigma1(x) (ROTR(x, 6) ^ ROTR(x, 11) ^ ROTR(x, 25))
// σ0函数
#define sigma0(x) (ROTR(x, 7) ^ ROTR(x, 18) ^ ((x) >> 3))
// σ1函数
#define sigma1(x) (ROTR(x, 17) ^ ROTR(x, 19) ^ ((x) >> 10))
// 消息填充
void sha256_pad(uint8_t *data, size_t len, uint8_t *padded, size_t *padded_len) {
size_t bit_len = len * 8;
size_t pad_len = (len % SHA256_BLOCK_SIZE < 56) ? (SHA256_BLOCK_SIZE - len % SHA256_BLOCK_SIZE) : (2 * SHA256_BLOCK_SIZE - len % SHA256_BLOCK_SIZE);
memcpy(padded, data, len);
padded[len] = 0x80; // 添加一个“1”位
// 填充“0”位
for (size_t i = len + 1; i < len + pad_len - 8; i++) {
padded[i] = 0x00;
}
// 添加64位的长度字段(大端序)
for (int i = 0; i < 8; i++) {
padded[len + pad_len - 8 + i] = (bit_len >> (56 - 8 * i)) & 0xFF;
}
*padded_len = len + pad_len;
}
// SHA-256压缩函数
void sha256_compress(uint32_t state[8], const uint8_t block[SHA256_BLOCK_SIZE]) {
uint32_t W[64];
uint32_t a, b, c, d, e, f, g, h;
uint32_t T1, T2;
// 初始化工作变量
a = state[0];
b = state[1];
c = state[2];
d = state[3];
e = state[4];
f = state[5];
g = state[6];
h = state[7];
// 扩展消息
for (int t = 0; t < 16; t++) {
W[t] = (block[t * 4] << 24) | (block[t * 4 + 1] << 16) | (block[t * 4 + 2] << 8) | block[t * 4 + 3];
}
for (int t = 16; t < 64; t++) {
W[t] = sigma1(W[t - 2]) + W[t - 7] + sigma0(W[t - 15]) + W[t - 16];
}
// 压缩函数
for (int t = 0; t < 64; t++) {
T1 = h + Sigma1(e) + Ch(e, f, g) + K[t] + W[t];
T2 = Sigma0(a) + Maj(a, b, c);
h = g;
g = f;
f = e;
e = d + T1;
d = c;
c = b;
b = a;
a = T1 + T2;
}
// 更新状态
state[0] += a;
state[1] += b;
state[2] += c;
state[3] += d;
state[4] += e;
state[5] += f;
state[6] += g;
state[7] += h;
}
// SHA-256主函数
void sha256(const uint8_t *data, size_t len, uint8_t hash[SHA256_DIGEST_SIZE]) {
uint8_t padded[SHA256_BLOCK_SIZE * 2];
size_t padded_len;
uint32_t state[8] = {
0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a,
0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19
};
// 消息填充
sha256_pad(data, len, padded, &padded_len);
// 处理每个块
for (size_t i = 0; i < padded_len; i += SHA256_BLOCK_SIZE) {
sha256_compress(state, padded + i);
}
// 生成最终散列值
for (int i = 0; i < 8; i++) {
hash[i * 4] = (state[i] >> 24) & 0xFF;
hash[i * 4 + 1] = (state[i] >> 16) & 0xFF;
hash[i * 4 + 2] = (state[i] >> 8) & 0xFF;
hash[i * 4 + 3] = state[i] & 0xFF;
}
}
// 打印散列值
void print_hash(const uint8_t hash[SHA256_DIGEST_SIZE]) {
for (int i = 0; i < SHA256_DIGEST_SIZE; i++) {
printf("%02x", hash[i]);
}
printf("\n");
}
// 测试
int main() {
const char *message = "Hello, SHA-256!";
uint8_t hash[SHA256_DIGEST_SIZE];
sha256((uint8_t *)message, strlen(message), hash);
printf("SHA-256: ");
print_hash(hash);
return 0;
}
4.逆向
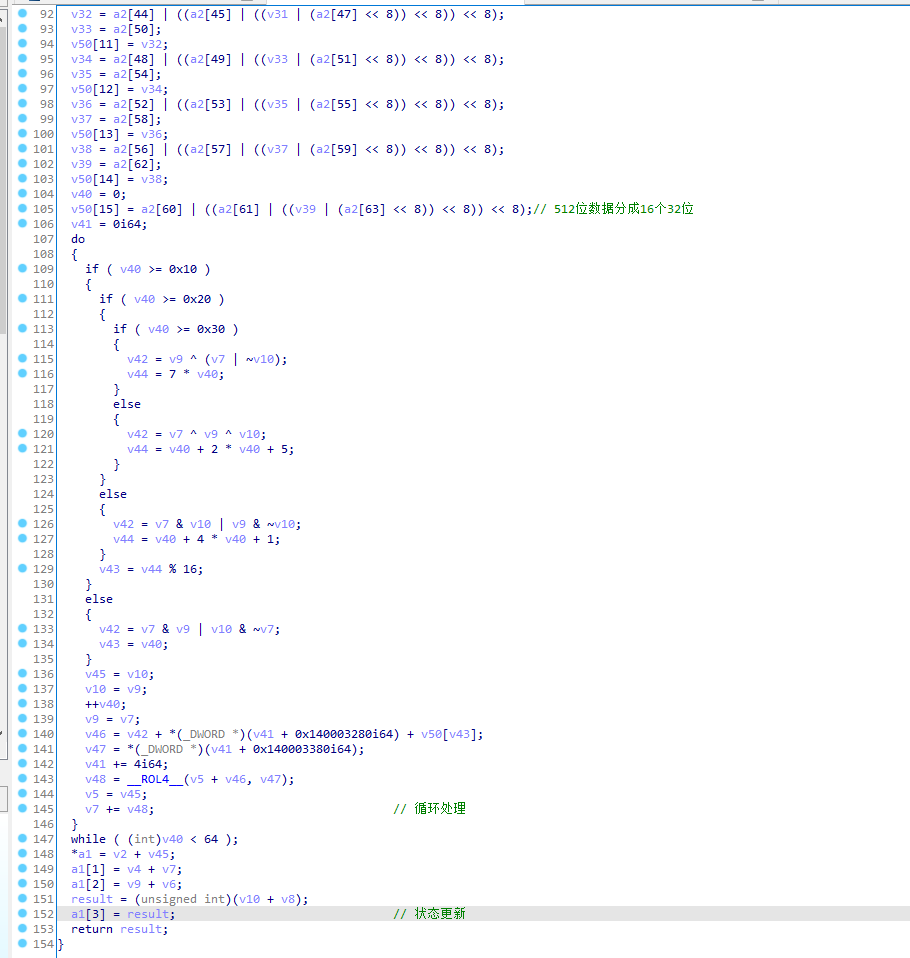
特点1:
8个初始化向量
H0 = 0x6a09e667
H1 = 0xbb67ae85
H2 = 0x3c6ef372
H3 = 0xa54ff53a
H4 = 0x510e527f
H5 = 0x9b05688c
H6 = 0x1f83d9ab
H7 = 0x5be0cd19

特点2:
循环处理
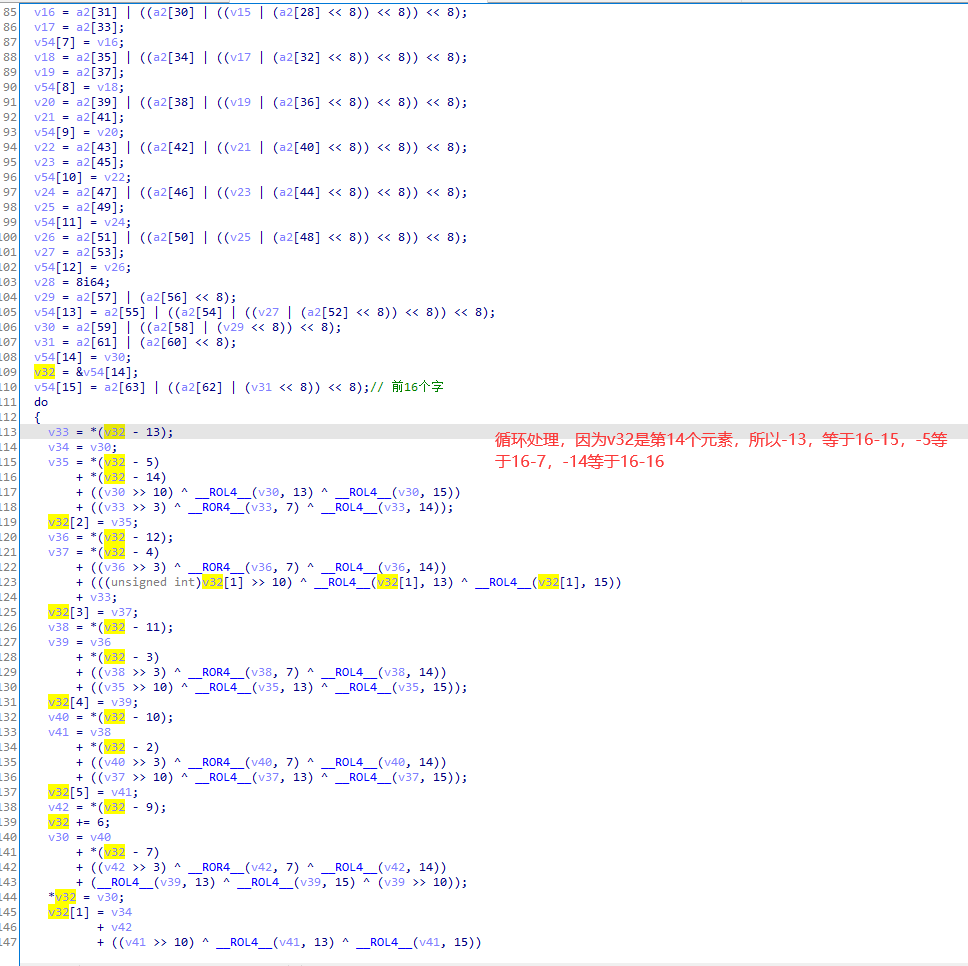
对应循环:

5. 魔改
1.修改SHA-256 初始向量。
2.修改64轮运算的次数,如增加至96轮,减少至32轮。
3.修改64轮运算的轮常量K。
1.3 RC4
1.简介
RC4,是Ron Rivest在1987年设计的流密码,它曾经被广泛使用,比如在SSL/TLS和WEP中,但现在因为各种漏洞已经被淘汰了。比如WEP的不安全性,很大一部分原因就是RC4的弱点。
2.算法实现
- 密钥生成
- 用0-255初始化S[255]数组,将密钥重复填充到255字节,用密钥打乱S。
- 生成密钥流
- 通过一定算法生成密钥流。
- 加密
- 密钥流与明文异或。
3.代码实现
#include <stdio.h>
#include <string.h>
typedef struct {
unsigned char S[256]; // 状态数组
int i, j; // 状态指针
} RC4_CTX;
// 密钥调度算法(KSA)
void rc4_init(RC4_CTX* ctx, const unsigned char* key, int key_len) {
ctx->i = ctx->j = 0;
// 初始化S盒
for (int i = 0; i < 256; i++) {
ctx->S[i] = i;
}
// 打乱S盒
int j = 0;
for (int i = 0; i < 256; i++) {
j = (j + ctx->S[i] + key[i % key_len]) % 256;
// 交换S[i]和S[j]
unsigned char temp = ctx->S[i];
ctx->S[i] = ctx->S[j];
ctx->S[j] = temp;
}
}
// 生成单个密钥流字节(PRGA)
unsigned char rc4_keystream_byte(RC4_CTX* ctx) {
ctx->i = (ctx->i + 1) % 256;
ctx->j = (ctx->j + ctx->S[ctx->i]) % 256;
// 交换S[i]和S[j]
unsigned char temp = ctx->S[ctx->i];
ctx->S[ctx->i] = ctx->S[ctx->j];
ctx->S[ctx->j] = temp;
// 计算密钥流字节
return ctx->S[(ctx->S[ctx->i] + ctx->S[ctx->j]) % 256];
}
// 加密/解密函数(RC4是对称操作)
void rc4_crypt(RC4_CTX* ctx, const unsigned char* input, unsigned char* output, int len) {
for (int k = 0; k < len; k++) {
output[k] = input[k] ^ rc4_keystream_byte(ctx);
}
}
// 示例用法
int main() {
// 密钥和明文
const char* key = "SecretKey";
const char* plaintext = "Hello, RC4!";
int len = strlen(plaintext);
// 加密
RC4_CTX ctx;
unsigned char ciphertext[256];
rc4_init(&ctx, (unsigned char*)key, strlen(key));
rc4_crypt(&ctx, (unsigned char*)plaintext, ciphertext, len);
printf("Ciphertext (Hex): ");
for (int i = 0; i < len; i++) {
printf("%02X ", ciphertext[i]);
}
printf("\n");
// 解密(重用密钥)
unsigned char decrypted[256];
rc4_init(&ctx, (unsigned char*)key, strlen(key)); // 重置状态
rc4_crypt(&ctx, ciphertext, decrypted, len);
decrypted[len] = '\0'; // 添加字符串结束符
printf("Decrypted Text: %s\n", decrypted);
return 0;
}
4.逆向
特点1:
KSA算法

特点2:
PRGA算法

1.3 RC4
1.简介
TEA 是一种 Feistel 网络(类似于 DES)结构的加密算法,它采用 32 位 的数据块和 128 位 的密钥(4 个 32 位子密钥),加密过程中会进行多轮迭代。TEA 加密算法的核心操作是基于异或(XOR)、加法和位移的运算。
2.算法实现
- 输入
- 将 64 位的数据块(v0, v1)和 128 位密钥(k0, k1, k2, k3)传入。
- 轮操作
- 对每一轮进行的操作使用了加法、异或和位移操作。通常进行 64 轮迭代操作(但实际可调节轮数,增加轮数可提高安全性)。
3.代码实现
#include <stdio.h>
#include <stdint.h>
#define DELTA 0x9e3779b9
void TEA_encrypt(uint32_t v[2], uint32_t k[4]) {
uint32_t sum = 0;
uint32_t v0 = v[0], v1 = v[1];
uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
for (int i = 0; i < 64; ++i) {
sum += DELTA;
v0 += (((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1));
v1 += (((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3));
}
v[0] = v0;
v[1] = v1;
}
void TEA_decrypt(uint32_t v[2], uint32_t k[4]) {
uint32_t sum = DELTA * 64;
uint32_t v0 = v[0], v1 = v[1];
uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
for (int i = 0; i < 64; ++i) {
v1 -= (((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3));
v0 -= (((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1));
sum -= DELTA;
}
v[0] = v0;
v[1] = v1;
}
int main() {
uint32_t v[2] = {0x01234567, 0x89abcdef};
uint32_t k[4] = {0x01234567, 0x89abcdef, 0x11111111, 0x22222222};
printf("Original data: v[0] = 0x%x, v[1] = 0x%x\n", v[0], v[1]);
TEA_encrypt(v, k);
printf("Encrypted data: v[0] = 0x%x, v[1] = 0x%x\n", v[0], v[1]);
TEA_decrypt(v, k);
printf("Decrypted data: v[0] = 0x%x, v[1] = 0x%x\n", v[0], v[1]);
return 0;
}
4.逆向
特点1:
+常数0x9e3779b9 或者-常数0x61C88647

特点2:
解密函数反过来-常数0x9e3779b9 或者+常数0x61C88647

1.4 IDEA
1.简介
IDEA是一种对称密钥分组密码算法,由瑞士学者来学嘉(Xuejia Lai)和James Massey于1991年提出。它以高安全性和高效性著称,曾用于PGP(Pretty Good Privacy)等加密工具中。
2.算法实现
- 子密钥生成
- 128位密钥生成52组子密钥。(每轮6个共八轮,最后一轮取前4个,循环右移)
- 分组处理
- 将64位明文分为4个16位子块(X₁, X₂, X₃, X₄)每轮操作如下:
- 模乘(⊗):与子密钥进行模 2^(16+1) 乘法(0视为2^16)。
- 模加(+):与子密钥进行模 2^ 加法。
- 异或(⊕):中间结果的混合。

- 输出变换
- 最后一轮后,使用4个子密钥对4个子块进行最终变换。
3.代码实现
#include<iostream>
#include<bitset>
#include<math.h>
using namespace std;
typedef bitset<16> code; //16位
typedef bitset<128> key; //128位秘钥
bitset<16> sub_key[52]; //52个子秘钥
bitset<16> inv_sub_key[52];//52个逆子秘钥
bitset<64> plaint_txt;
//异或运算
code XOR(code code_1, code code_2)
{
return code_1 ^ code_2;
}
//加法运算
code Plus(code code_1, code code_2)
{
int tmp = 0;
code result;
for (int i = 0; i < 16; i++) //二进制转换成十进制
{
tmp += code_1[i] * pow(2, i) + code_2[i] * pow(2, i);
}
tmp %= 65536;
bitset<16>binary(tmp); //转换成二进制
for (int i = 0; i < 16; i++)
result[i] = binary[i];
return result;
}
//逆加法
code invPlus(code code_in)
{
int tmp = 0;
code result;
for (int i = 0; i < 16; i++) //二进制转换成十进制
tmp += code_in[i] * pow(2, i);
tmp = 65536 - tmp;
bitset<16>binary(tmp); //转换成二进制
for (int i = 0; i < 16; i++)
result[i] = binary[i];
return result;
}
//乘法运算
code Times(code code_1, code code_2)
{
code result;
long long tmp;
long long tmp_1 = 0, tmp_2 = 0;
for (int i = 0; i < 16; i++) //二进制转换成十进制
{
tmp_1 += code_1[i] * pow(2, i);
tmp_2 += code_2[i] * pow(2, i);
}
if (code_1 == 0)
tmp_1 = 65536;
if (code_2 == 0)
tmp_2 = 65536;
tmp = (tmp_1 * tmp_2) % 65537;
if (tmp == 65536) //如果得到最大值即等价于0x0000
result = 0x0000;
else
{
bitset<16>binary(tmp); //转换成二进制
for (int i = 0; i < 16; i++)
result[i] = binary[i];
}
return result;
}
void Exgcd(int a, int b, int& x, int& y) //欧几里得扩展算法
{
if (!b)
x = 1, y = 0;
else
Exgcd(b, a % b, y, x), y -= a / b * x;
}
//利用欧几里得扩展算法求乘法的逆
code invTimes(code code_in)
{
code result;
int tmp = 0;
for (int i = 0; i < 16; i++) //首先转换成十进制
tmp += code_in[i] * pow(2, i);
int x, y;
int p = 65537;
Exgcd(tmp, p, x, y);
x = (x % p + p) % p; //x即为tmp在 (mod65537) 的乘法逆
bitset<16>binary(x); //转换成二进制
for (int j = 0; j < 16; j++)
result[j] = binary[j];
return result;
}
//子秘钥生成
void subkeys_get(code keys_input[8])//输入8个16bit组
{
key keys;
for (int i = 0; i < 8; i++) //转化成128位
{
for (int j = 0; j < 16; j++)
{
keys[j + 16 * i] = keys_input[7 - i][j];
}
}
for (int i = 0; i < 8; i++) //前8个子秘钥(不移动)
{
for (int j = 0; j < 16; j++)
sub_key[i][15 - j] = keys[127 - (j + 16 * i)];
}
for (int i = 0; i < 5; i++) //中间40个子秘钥()每次循环左移25位
{
key tmp_keys = keys >> 103;
keys = (keys << 25) | (tmp_keys);
for (int j = (8 + 8 * i); j < (8 * (i + 2)); j++)
{
for (int k = 0; k < 16; k++)
sub_key[j][15 - k] = keys[127 - (k + 16 * (j - 8 - 8 * i))];
}
}
key tmp_keys = keys >> 103; //最后一次循环左移取前四个
keys = (keys << 25) | (tmp_keys);
for (int i = 48; i < 52; i++)
{
for (int j = 0; j < 16; j++)
sub_key[i][15 - j] = keys[127 - (j + 16 * (i - 48))];
}
}
void inv_subkeys_get(code sub_key[52]) //将52个子秘钥调用
{
//生成逆子秘钥
for (int i = 6; i < 48; i = i + 6) //U_1, U_2, U_3, U_4 (2 <= i <= 8)
{
inv_sub_key[i] = invTimes(sub_key[48 - i]);
inv_sub_key[i + 1] = invPlus(sub_key[50 - i]);
inv_sub_key[i + 2] = invPlus(sub_key[49 - i]);
inv_sub_key[i + 3] = invTimes(sub_key[51 - i]);
}
for (int i = 0; i < 48; i = i + 6) //U_5, U_6 (1 <= i <= 8)
{
inv_sub_key[i + 4] = sub_key[46 - i];
inv_sub_key[i + 5] = sub_key[47 - i];
}
//U_1, U_2, U_3, U_4 (i = 1, 9)
inv_sub_key[0] = invTimes(sub_key[48]);
inv_sub_key[1] = invPlus(sub_key[49]);
inv_sub_key[2] = invPlus(sub_key[50]);
inv_sub_key[3] = invTimes(sub_key[51]);
inv_sub_key[48] = invTimes(sub_key[0]);
inv_sub_key[49] = invPlus(sub_key[1]);
inv_sub_key[50] = invPlus(sub_key[2]);
inv_sub_key[51] = invTimes(sub_key[3]);
}
//加密
bitset<64> encrypt(bitset<64> plaint)
{
bitset<16> I_1, I_2, I_3, I_4;
bitset<64> cipher;
for (int i = 0; i < 16; i++) //明文分成4个16位(I_1, I_2, I_3, I_4)
{
I_1[15 - i] = plaint[63 - i];
I_2[15 - i] = plaint[47 - i];
I_3[15 - i] = plaint[31 - i];
I_4[15 - i] = plaint[15 - i];
}
for (int i = 0; i < 48; i = i + 6) //轮结构运算
{
bitset<16> tmp_1 = Times(sub_key[i], I_1);
bitset<16> tmp_2 = Plus(sub_key[i + 1], I_2);
bitset<16> tmp_3 = Plus(sub_key[i + 2], I_3);
bitset<16> tmp_4 = Times(sub_key[i + 3], I_4);
bitset<16> tmp_5 = XOR(tmp_1, tmp_3);
bitset<16> tmp_6 = XOR(tmp_2, tmp_4);
bitset<16> tmp_7 = Times(sub_key[i + 4], tmp_5);
bitset<16> tmp_8 = Plus(tmp_6, tmp_7);
bitset<16> tmp_9 = Times(tmp_8, sub_key[i + 5]);
bitset<16> tmp_10 = Plus(tmp_7, tmp_9);
I_1 = XOR(tmp_1, tmp_9);
I_2 = XOR(tmp_3, tmp_9);
I_3 = XOR(tmp_2, tmp_10);
I_4 = XOR(tmp_4, tmp_10);
}
//输出变换
bitset<16> Y_1 = Times(I_1, sub_key[48]);
bitset<16> Y_2 = Plus(I_3, sub_key[49]);
bitset<16> Y_3 = Plus(I_2, sub_key[50]);
bitset<16> Y_4 = Times(I_4, sub_key[51]);
for (int i = 0; i < 16; i++) //整合4个输出成密文
{
cipher[i] = Y_4[i];
cipher[i + 16] = Y_3[i];
cipher[i + 32] = Y_2[i];
cipher[i + 48] = Y_1[i];
}
return cipher;
}
//解密(过程与加密一致,子秘钥变成逆子秘钥)
bitset<64> dencrypt(bitset<64> cipher)
{
//解密
bitset<16> I_1, I_2, I_3, I_4;
bitset<64> plaint;
for (int i = 0; i < 16; i++)
{
I_1[15 - i] = cipher[63 - i];
I_2[15 - i] = cipher[47 - i];
I_3[15 - i] = cipher[31 - i];
I_4[i] = cipher[i];
}
for (int i = 0; i < 48; i = i + 6)
{
bitset<16> tmp_1 = Times(inv_sub_key[i], I_1);
bitset<16> tmp_2 = Plus(inv_sub_key[i + 1], I_2);
bitset<16> tmp_3 = Plus(inv_sub_key[i + 2], I_3);
bitset<16> tmp_4 = Times(inv_sub_key[i + 3], I_4);
bitset<16> tmp_5 = XOR(tmp_1, tmp_3);
bitset<16> tmp_6 = XOR(tmp_2, tmp_4);
bitset<16> tmp_7 = Times(inv_sub_key[i + 4], tmp_5);
bitset<16> tmp_8 = Plus(tmp_6, tmp_7);
bitset<16> tmp_9 = Times(tmp_8, inv_sub_key[i + 5]);
bitset<16> tmp_10 = Plus(tmp_7, tmp_9);
I_1 = XOR(tmp_1, tmp_9);
I_2 = XOR(tmp_3, tmp_9);
I_3 = XOR(tmp_2, tmp_10);
I_4 = XOR(tmp_4, tmp_10);
}
bitset<16> Y_1 = Times(I_1, inv_sub_key[48]);
bitset<16> Y_2 = Plus(I_3, inv_sub_key[49]);
bitset<16> Y_3 = Plus(I_2, inv_sub_key[50]);
bitset<16> Y_4 = Times(I_4, inv_sub_key[51]);
for (int i = 0; i < 16; i++)
{
plaint[i] = Y_4[i];
plaint[i + 16] = Y_3[i];
plaint[i + 32] = Y_2[i];
plaint[i + 48] = Y_1[i];
}
return plaint;
}
int main()
{
plaint_txt = 0xa6224adf2f28df73;//64位明文
//plaint_txt = 0xa795 8723 1f2c 6d73 ;
cout << "明文:" << endl << plaint_txt << endl;
code keys_input[8] = { 0x151a, 0x048b, 0x71a1, 0xf9c7, 0x5266, 0xbfd6, 0x24a2, 0xdff1 };//128位秘钥
subkeys_get(keys_input); //生成子秘钥
inv_subkeys_get(sub_key);//生成逆子秘钥
bitset<64> cipher = encrypt(plaint_txt); //加密得到密文cipher
cout << "加密得到的密文为:" << endl << cipher << endl;
bitset<64> plaint = dencrypt(cipher); //解密得到明文plaint
cout << "解密得到:" << endl << plaint << endl;
return 0;
}
4.逆向
特点1:
循环左移25
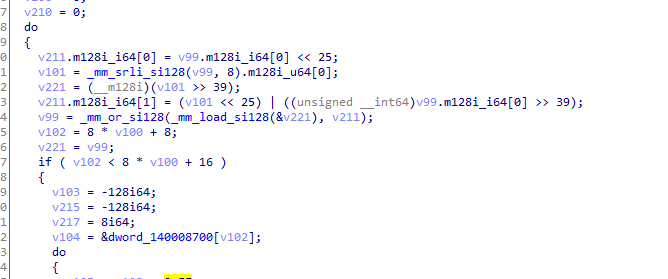
特点2:
欧几里得算法求模乘逆元:
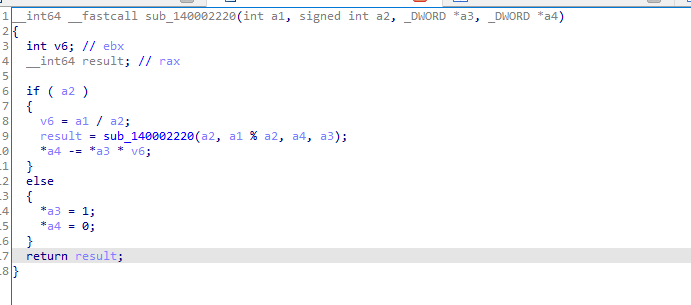
特点3:对于65537的模乘

1.5 blowfish
1.简介
Blowfish是一种对称密钥分组加密算法,由密码学家Bruce Schneier于1993年设计,旨在替代当时存在安全缺陷的DES(Data Encryption Standard)算法。它以其高效性、灵活性和免费开源的特点广受欢迎,尤其适用于旧系统或资源受限的环境。
2.算法实现
- 密钥生成
- P-box由18个32位的子密钥组成,并且有S-box包含1024个32位数据(S[4][256]),使用Π的小数部分初始化S-box和P-box,将用户提供的密钥按位异或到P-box中(循环使用密钥字节)。用当前的P-box和S-box加密一个全零块,并用结果更新P-box和S-box。
- 加密
- 每轮操作将64位明文分为左右两半(L和R,各32位),经过16轮迭代:
- 输入:64位明文分为L₀和R₀。
- 轮函数(F函数):
- 将32位的R输入到F函数,分为4个8位块(a, b, c, d)。
- 查询4个S-box:F(R) = (S₁[a] + S₂[b]) XOR S₃[c] + S₄[d](模2³²)。
3.代码实现
#include "BlowFish.h"
#include <string>
using namespace std;
bool BlowFishInit(BLOWFISH_CTX* blowCtx, unsigned char* key, unsigned int keylen)
{
//设置传入的CTX中的SBOX值
for (int Row = 0; Row < 4; Row++)
{
for (int Col = 0; Col < 256; Col++)
{
blowCtx->sbox[Row][Col] = ORIG_S[Row][Col];
}
}
/*
设置pbox
1.循环18轮
2.每轮都设置ctx.pbox值与data ^
3.data = *(DWORD*)key[0] key[1].....
*/
int KeyIndex = 0;
for (int index = 0; index < N + 2; index++)
{
unsigned int data = 0;
//填充data 将key的字符设置到data当中
for (int k = 0; k < 4; k++)
{
//通过移位设置每个字符
data = (data << 8) | key[KeyIndex];
KeyIndex++;
//如果超出了key长度 那么key要从开始
if (KeyIndex >= keylen)
KeyIndex = 0;
}
//否则不满足
blowCtx->pbox[index] = ORIG_P[index] ^ data;
}
//对一个64位0 进行加密。加密结果的输出设置到pbox[i]与pbox[i+1]中
unsigned int Data1 = 0;
unsigned int Data2 = 0;
for (int i = 0; i < N + 2; i += 2)
{
BlowFish_Encry(blowCtx, &Data1, &Data2);
blowCtx->pbox[i] = Data1;
blowCtx->pbox[i + 1] = Data2;
}
//初始化Sbox
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 256; j += 2)
{
BlowFish_Encry(blowCtx, &Data1, &Data2);
blowCtx->sbox[i][j] = Data1;
blowCtx->sbox[i][j + 1] = Data2;
}
}
return true;
}
//unsigned int F(PBLOWFISH_CTX blowCtx, unsigned int Data)
//{
//
// unsigned int a, b, c, d;
// /*
// 利用位运算 取出下标值
// */
//
// a = (Data >> 24) & 0xFF;
// b = (Data >> 16) & 0xFF;
// c = (Data >> 8) & 0xFf;
// d = Data & 0xFF;
//
//
// int TempValue = blowCtx->sbox[0][a] + blowCtx->sbox[1][b];
// TempValue = TempValue ^ blowCtx->sbox[2][c];
// TempValue = TempValue + blowCtx->sbox[3][d];
// //公式 ((a+b)^c)+d
// return TempValue;
//}
static unsigned long F(BLOWFISH_CTX* ctx, unsigned long x) {
unsigned short a, b, c, d;
unsigned long y;
/* d = (unsigned short)(x & 0xFF);
x >>= 8;
c = (unsigned short)(x & 0xFF);
x >>= 8;
b = (unsigned short)(x & 0xFF);
x >>= 8;
a = (unsigned short)(x & 0xFF);
//都可以使用
*/
a = (x >> 24) & 0xFF;
b = (x >> 16) & 0xFF;
c = (x >> 8) & 0xFf;
d = x & 0xFF;
y = ctx->sbox[0][a] + ctx->sbox[1][b];
y = y ^ ctx->sbox[2][c];
y = y + ctx->sbox[3][d];
return y;
}
void BlowFish_Encry(PBLOWFISH_CTX blowCtx, unsigned int* left, unsigned int* right)
{
unsigned long Xl;
unsigned long Xr;
unsigned long temp;
short i;
//加密部分首先将其分为left跟right两组。 每一组分别32位
Xl = *left;
Xr = *right;
for (i = 0; i < N; ++i) {
Xl = Xl ^ blowCtx->pbox[i];
Xr = F(blowCtx, Xl) ^ Xr;
temp = Xl;
Xl = Xr; //交换左右的值。 l = R r= l 继续下一轮循环。总共16轮
Xr = temp;
}
temp = Xl;
Xl = Xr; //16轮完毕之后交换变量
Xr = temp;
Xr = Xr ^ blowCtx->pbox[N]; //最后进行一次疑或
Xl = Xl ^ blowCtx->pbox[N + 1];
*left = Xl;
*right = Xr;
}
void BlowFish_Decrypt(PBLOWFISH_CTX blowCtx, unsigned int* left, unsigned int* right)
{
unsigned int Xl = *left;
unsigned int Xr = *right;
//倒着循环
for (int i = N + 1; i > 1; --i)
{
Xl = Xl ^ blowCtx->pbox[i];
Xr = Xr ^ F(blowCtx, Xl);
//继续左右交换
unsigned int temp = Xl;
Xl = Xr;
Xr = temp;
}
//最后一轮继续交换
unsigned int temp = Xl;
Xl = Xr;
Xr = temp;
//返还原
Xr = Xr ^ blowCtx->pbox[1];
Xl = Xl ^ blowCtx->pbox[0];
//设置变量返回
*left = Xl;
*right = Xr;
}
int main()
{
unsigned int L = 1, R = 2;
BLOWFISH_CTX ctx;
BlowFishInit(&ctx, (unsigned char*)"IBinary", strlen("IBinary"));
BlowFish_Encry(&ctx, &L, &R);
BlowFish_Decrypt(&ctx, &L, &R);
}
4.逆向
特征1:4*256个32位数据的S-box

特征2:初始密钥异或18组的P-box

特征3:加密算法 16轮完毕之后交换变量再进行两次异或

1.6 DES
1.简介
DES(Data Encryption Standard,数据加密标准)是一种经典的对称加密算法,由IBM在1970年代设计,1977年被美国国家标准局(现NIST)正式采纳为联邦标准。目前已被AES(Advanced Encryption Standard)取代。
2.算法实现
- 密钥调度
- 首先从初始密钥(56位,但是每8位有一个奇偶校验位,所以是64位)计算出16个子密钥。
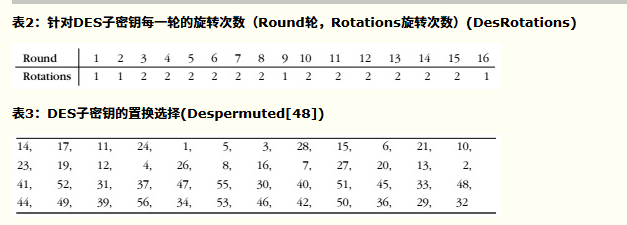
- 按照从左往右从上往下的方式看,表格中每个位置P包含初始密钥中位在转换后的密钥中所占的位置。比如,初始密钥中的第57位就是转换后的密钥中的第1位,而初始密钥中的第49位则变成转换后的密钥中的第2位,以此类推...。(数据位的计数顺序按照从左到右从1开始的)

- 将密钥转换为56位后,接下来计算子密钥。首先,将56位的密钥分为两个28位的组。然后,针对每个子密钥,根据子密钥的序列值旋转这两组值,然后重新合并。之后,再按照表3所示对重组后的密钥进行置换,使56位的子密钥缩小为48位。这个排列过程就称为置换选择。针对16个子密钥,每个子密钥重复一次该过程。这里的目的是保证将初始密钥中的不同位在每一轮排列后应用于加密的数据上。
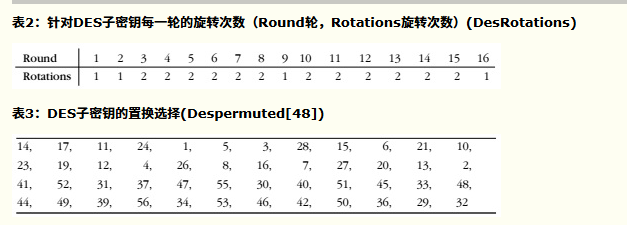
- 总过程如下图:
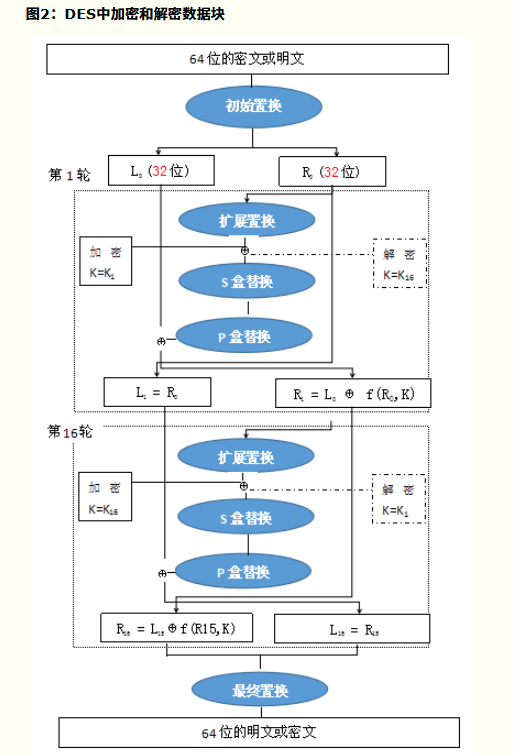
- 加密
- 首先按照如下图置换数据块,随后将数据分为两个32位的组L0和R0

- 完成初始置换后,数据块将重复执行16轮一系列的操作。每一轮操作(i)的目的是计算出Li和Ri ,这些结果将用在下一轮操作中直到最终得到数据R16和L16。
- 每一轮以Li-1和Ri-1开始,然后根据表5所示进行扩展置换,将Ri-1从32位扩展到48位。

- 再将计算的Rint通过8个单独的S盒进行替换操作,S盒操作通过将48位数据分成8组,在8个S盒中替换成对应数据(数据为4位),最后变成了32位数据。
- 最后再将32位数据进行P盒替换。

- 最后再对结果R16L16进行最终置换(初始置换的逆过程)总流程如图:
3.代码实现
#include <stdlib.h>
#include <stdio.h>
#include "DEStable.h"
#include "des.h"
/**
* Feistel 轮函数,用于进行16次迭代
* @param R 32位数据
* @param K 48位子密钥
* @param output 32位输出
*/
void Feistel(bool* R, bool* K, bool* output) {
// 1) 将32位的串R作E-扩展,成为48位的串
int i;
bool expandR[48];
for (i = 0; i < 48; ++i)
{
expandR[i] = R[E[i] - 1];
}
// 2) expandR 与 K 异或
for (i = 0; i < 48; ++i)
{
expandR[i] = expandR[i] == K[i] ? 0 : 1;
}
// 3) 用S-盒分别对8个组进行 6-4 转换
bool temp[32];
for (i = 0; i < 8; ++i)
{
int j = i * 6;
int row = expandR[j] * 2 + expandR[j + 5];
int col = expandR[j + 1] * 8 + expandR[j + 2] * 4 + expandR[j + 3] * 2 + expandR[j + 4];
int num = S_BOX[i][row][col];
j = i * 4;
int k;
for (k = 3; k >= 0; --k)
{
temp[j + k] = num % 2;
num /= 2;
}
}
// 4) P-置换
for (i = 0; i < 32; ++i)
{
output[i] = temp[P[i] - 1];
}
return;
}
/**
* 对56位密钥的前后部分进行左移
* @param A 56位密钥
* @param shift 偏移量
*/
void LeftShift(bool* A, int shift) {
int temp0 = A[0], temp1 = A[1];
int i;
for (i = 0; i < 26; ++i) {
A[i] = A[i + shift];
}
if (shift == 1) {
A[26] = A[27];
A[27] = temp0;
}
else if (shift == 2) {
A[26] = temp0;
A[27] = temp1;
}
}
/**
* 生成16个48位的子密钥
*/
void GenerateSubKeys() {
bool realKey[56];
bool left[28];
bool right[28];
int i;
// 对密钥的56个非校验位实行PC-1置换
for (i = 0; i < 56; ++i)
{
realKey[i] = key[PC_1[i] - 1];
}
// 生成子密钥并保存
for (i = 0; i < 16; ++i)
{
int j;
// 提取realKey的前28位和后28位
for (j = 0; j < 28; ++j)
{
left[j] = realKey[j];
}
for (j = 0; j < 28; ++j)
{
right[j] = realKey[j + 28];
}
// 左移
LeftShift(left, shiftBits[i]);
LeftShift(right, shiftBits[i]);
// 恢复
for (j = 0; j < 28; ++j)
{
realKey[j] = left[j];
}
for (j = 0; j < 28; ++j)
{
realKey[j] = right[j + 28];
}
// PC-2压缩置换
for (j = 0; j < 48; ++j)
{
subKey[i][j] = realKey[PC_2[j] - 1];
}
}
}
/**
* DES加密
* @param plain 明文
* @param cipher 加密得到的密文
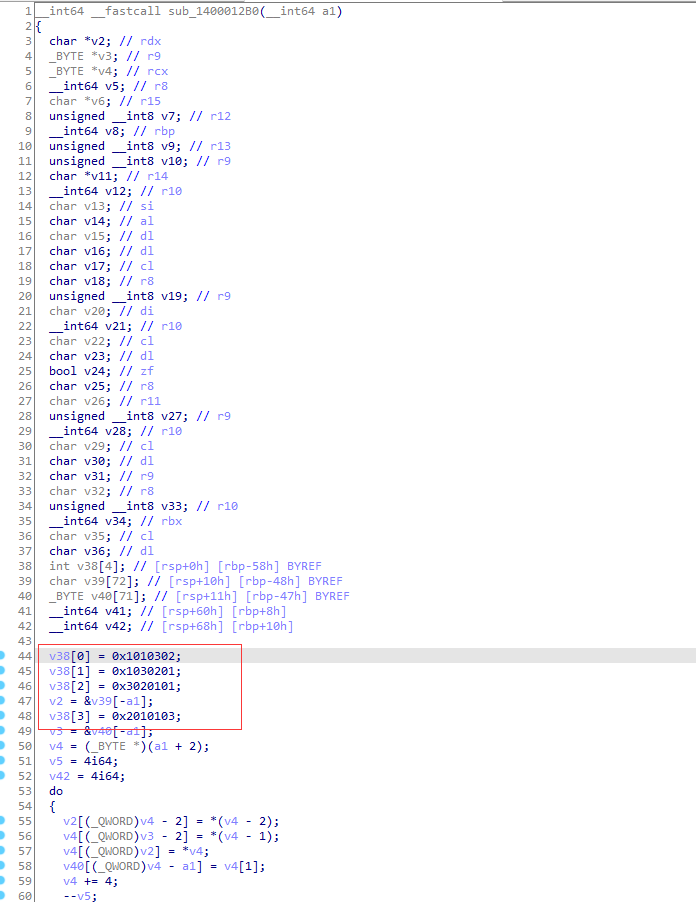
*/
void encrypt(bool* plain, bool* cipher) {
bool temp[64];
bool left[32];
bool right[32];
bool newLeft[32];
int i, round;
// 1) 初始置换IP
for (i = 0; i < 64; ++i)
{
temp[i] = plain[IP[i] - 1];
}
// 2) 16轮迭代
for (i = 0; i < 32; ++i)
{
left[i] = temp[i];
}
for (i = 0; i < 32; ++i)
{
right[i] = temp[i + 32];
}
for (round = 0; round < 16; ++round)
{
for (i = 0; i < 32; ++i)
{
newLeft[i] = right[i];
}
bool fresult[32];
Feistel(right, subKey[round], fresult);
for (i = 0; i < 32; ++i)
{
right[i] = left[i] == fresult[i] ? 0 : 1;
}
for (i = 0; i < 32; ++i)
{
left[i] = newLeft[i];
}
}
// 3) 交换置换
for (i = 0; i < 32; ++i)
{
temp[i] = right[i];
}
for (i = 0; i < 32; ++i)
{
temp[i + 32] = left[i];
}
// 4) 逆置换
for (i = 0; i < 64; ++i)
{
cipher[i] = temp[IP_1[i] - 1];
}
return;
}
/**
* DES解密
* @param cipher 密文
* @param plain 解密得到的明文
*/
void decrypt(bool* cipher, bool* plain) {
bool temp[64];
bool left[32];
bool right[32];
bool newLeft[32];
int i, round;
// 1) 初始置换IP
for (i = 0; i < 64; ++i)
{
temp[i] = cipher[IP[i] - 1];
}
// 2) 16轮迭代
for (i = 0; i < 32; ++i)
{
left[i] = temp[i];
}
for (i = 0; i < 32; ++i)
{
right[i] = temp[i + 32];
}
for (round = 0; round < 16; ++round)
{
for (i = 0; i < 32; ++i)
{
newLeft[i] = right[i];
}
bool fresult[32];
Feistel(right, subKey[15 - round], fresult);
for (i = 0; i < 32; ++i)
{
right[i] = left[i] == fresult[i] ? 0 : 1;
}
for (i = 0; i < 32; ++i)
{
left[i] = newLeft[i];
}
}
// 3) 交换置换
for (i = 0; i < 32; ++i)
{
temp[i] = right[i];
}
for (i = 0; i < 32; ++i)
{
temp[i + 32] = left[i];
}
// 4) 逆置换
for (i = 0; i < 64; ++i)
{
plain[i] = temp[IP_1[i] - 1];
}
return;
}
/**
* 将8个字节转换成64位
* @param s 8个字节的char数组
* @param bitset 位数组
*/
void BytesToBits(char* s, bool* bitset) {
int i, j;
for (i = 0; i < 8; ++i)
{
for (j = 0; j < 8; ++j)
{
bitset[8 * i + j] = (s[i] >> j) & 1;
}
}
return;
}
void BitsToBytes(bool* bitset, char* s) {
int i, j;
for (i = 0; i < 8; ++i)
{
for (j = 0; j < 8; ++j)
{
s[i] |= ((int)bitset[8 * i + j]) << j;
}
}
s[8] = '\0';
return;
}
4.逆向
特征1:
置换成56位密钥后分成两个28位。

特征2:
根据轮次左移

特征3:
16轮子密钥生成,最后进行压缩置换。

特征4:
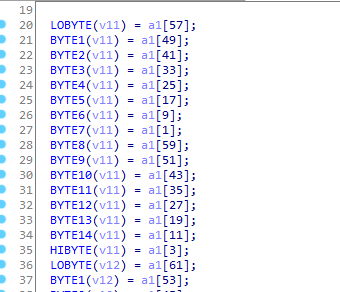
64位明文进行置换(v11-v14一个放16位):
特征5:
置换后明文分为两个32位

特征6:
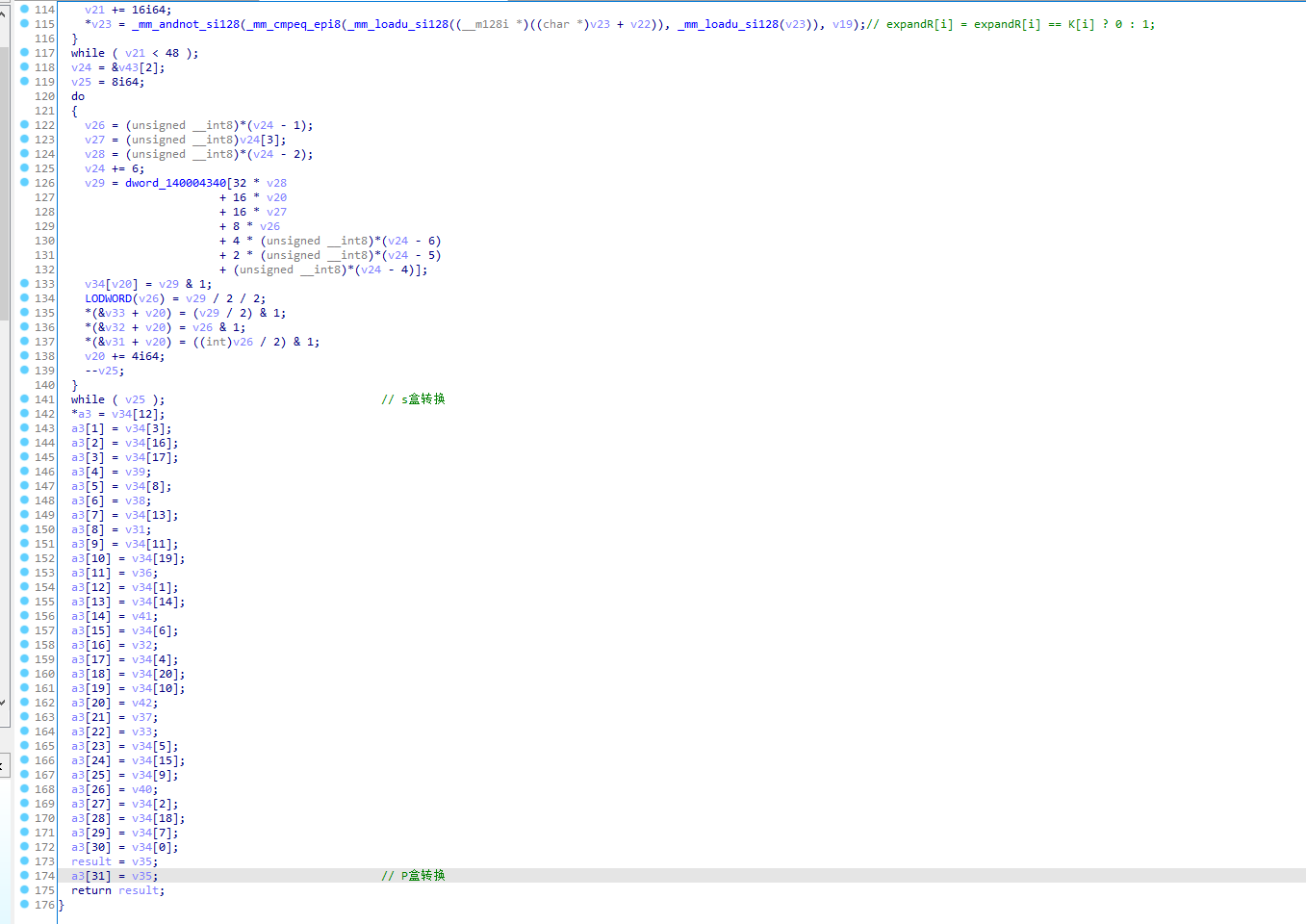
加密算法的S盒6-4,和P盒转换
1.7 AES
1.简介
AES 是一种对称密钥分组密码算法,由美国国家标准与技术研究院(NIST)于 2001 年发布,用于替代易受暴力破解攻击的 DES(数据加密标准)。它被广泛应用于政府、金融和日常互联网服务中,是当前最主流的加密算法之一。
2.算法实现
- 初始密钥轮加
- 输入数据块与种子密钥进行异或运算
- 主循环轮
- 字节替换
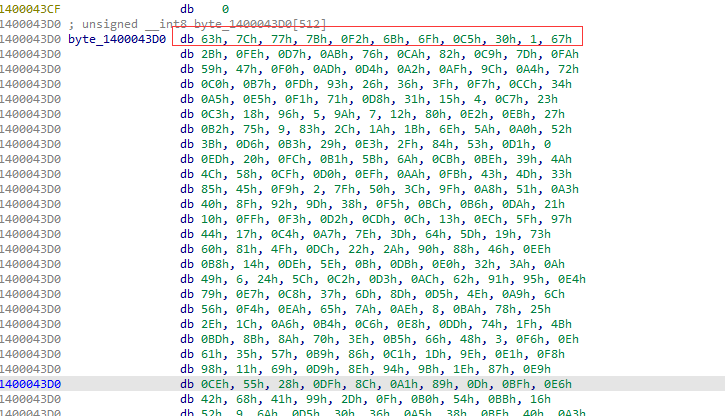
- 以高4位为行标,低4位为列标通过S-box混淆字节。
AES S盒(16x16 查找表)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0x63 | 0x7C | 0x77 | 0x7B | 0xF2 | 0x6B | 0x6F | 0xC5 | 0x30 | 0x01 | 0x67 | 0x2B | 0xFE | 0xD7 | 0xAB | 0x76 |
| 1 | 0xCA | 0x82 | 0xC9 | 0x7D | 0xFA | 0x59 | 0x47 | 0xF0 | 0xAD | 0xD4 | 0xA2 | 0xAF | 0x9C | 0xA4 | 0x72 | 0xC0 |
| 2 | 0xB7 | 0xFD | 0x93 | 0x26 | 0x36 | 0x3F | 0xF7 | 0xCC | 0x34 | 0xA5 | 0xE5 | 0xF1 | 0x71 | 0xD8 | 0x31 | 0x15 |
| 3 | 0x04 | 0xC7 | 0x23 | 0xC3 | 0x18 | 0x96 | 0x05 | 0x9A | 0x07 | 0x12 | 0x80 | 0xE2 | 0xEB | 0x27 | 0xB2 | 0x75 |
| 4 | 0x09 | 0x83 | 0x2C | 0x1A | 0x1B | 0x6E | 0x5A | 0xA0 | 0x52 | 0x3B | 0xD6 | 0xB3 | 0x29 | 0xE3 | 0x2F | 0x84 |
| 5 | 0x53 | 0xD1 | 0x00 | 0xED | 0x20 | 0xFC | 0xB1 | 0x5B | 0x6A | 0xCB | 0xBE | 0x39 | 0x4A | 0x4C | 0x58 | 0xCF |
| 6 | 0xD0 | 0xEF | 0xAA | 0xFB | 0x43 | 0x4D | 0x33 | 0x85 | 0x45 | 0xF9 | 0x02 | 0x7F | 0x50 | 0x3C | 0x9F | 0xA8 |
| 7 | 0x51 | 0xA3 | 0x40 | 0x8F | 0x92 | 0x9D | 0x38 | 0xF5 | 0xBC | 0xB6 | 0xDA | 0x21 | 0x10 | 0xFF | 0xF3 | 0xD2 |
| 8 | 0xCD | 0x0C | 0x13 | 0xEC | 0x5F | 0x97 | 0x44 | 0x17 | 0xC4 | 0xA7 | 0x7E | 0x3D | 0x64 | 0x5D | 0x19 | 0x73 |
| 9 | 0x60 | 0x81 | 0x4F | 0xDC | 0x22 | 0x2A | 0x90 | 0x88 | 0x46 | 0xEE | 0xB8 | 0x14 | 0xDE | 0x5E | 0x0B | 0xDB |
| A | 0xE0 | 0x32 | 0x3A | 0x0A | 0x49 | 0x06 | 0x24 | 0x5C | 0xC2 | 0xD3 | 0xAC | 0x62 | 0x91 | 0x95 | 0xE4 | 0x79 |
| B | 0xE7 | 0xC8 | 0x37 | 0x6D | 0x8D | 0xD5 | 0x4E | 0xA9 | 0x6C | 0x56 | 0xF4 | 0xEA | 0x65 | 0x7A | 0xAE | 0x08 |
| C | 0xBA | 0x78 | 0x25 | 0x2E | 0x1C | 0xA6 | 0xB4 | 0xC6 | 0xE8 | 0xDD | 0x74 | 0x1F | 0x4B | 0xBD | 0x8B | 0x8A |
| D | 0x70 | 0x3E | 0xB5 | 0x66 | 0x48 | 0x03 | 0xF6 | 0x0E | 0x61 | 0x35 | 0x57 | 0xB9 | 0x86 | 0xC1 | 0x1D | 0x9E |
| E | 0xE1 | 0xF8 | 0x98 | 0x11 | 0x69 | 0xD9 | 0x8E | 0x94 | 0x9B | 0x1E | 0x87 | 0xE9 | 0xCE | 0x55 | 0x28 | 0xDF |
| F | 0x8C | 0xA1 | 0x89 | 0x0D | 0xBF | 0xE6 | 0x42 | 0x68 | 0x41 | 0x99 | 0x2D | 0x0F | 0xB0 | 0x54 | 0xBB | 0x16 |
-
- 行移位
- 状态数组第一行不变,第二行循环左移1字节,第三行循环左移2字节,第四行循环左移3字节。
- 列混淆
- 在伽罗瓦域(GF(2⁸))中通过矩阵乘法混合列数据。
- [ 02 03 01 01 ]
矩阵 = [ 01 02 03 01 ]
[ 01 01 02 03 ]
[ 03 01 01 02 ] - 轮密钥加
- 与当前轮密钥进行异或
- 最终论
- 依次执行字节替换,行移位,轮密钥加
- 密钥扩展
- 循环移位
- 如果i=4的倍数,w[i]=w[i-1]循环左移一字节
- 字节替换
- 对w[i]根据S盒进行替换
- 轮常量异或
- w[i]=w[i-1]⊕w[i]⊕Rcon[j] j(从1开始)代表轮次,i(从0开始)代表第几个密钥
- 如果非4的倍数w[i]=w[i-4]⊕w[i-1]
3.代码实现
//
// Created by Liming Shao on 2018/4/24.
//
#include "AES.h"
#include <stdio.h>
#include <string.h>
#ifndef AES_UTILS_H
#define AES_UTILS_H
#include <stdint.h>
void printHex(const uint8_t* ptr, int len, const char* tag);
void printState(uint8_t state[4][4], const char* tag);
#endif //AES_UTILS_H
#define BLOCKSIZE 16
void printHex(const uint8_t* ptr, int len,const char* tag) {
printf("%s\ndata[%d]: ", tag, len);
for (int i = 0; i < len; ++i) {
printf("%.2X ", *ptr++);
}
printf("\n");
}
void printState(uint8_t(*state)[4],const char* tag) {
printf("%s\n", tag);
for (int i = 0; i < 4; ++i) {
printf("%.2X %.2X %.2X %.2X\n", state[i][0], state[i][1], state[i][2], state[i][3]);
}
printf("\n");
}
#define LOAD32H(x, y) \
do { (x) = ((uint32_t)((y)[0] & 0xff)<<24) | ((uint32_t)((y)[1] & 0xff)<<16) | \
((uint32_t)((y)[2] & 0xff)<<8) | ((uint32_t)((y)[3] & 0xff));} while(0)
#define STORE32H(x, y) \
do { (y)[0] = (uint8_t)(((x)>>24) & 0xff); (y)[1] = (uint8_t)(((x)>>16) & 0xff); \
(y)[2] = (uint8_t)(((x)>>8) & 0xff); (y)[3] = (uint8_t)((x) & 0xff); } while(0)
/* extract a byte */
#define BYTE(x, n) (((x) >> (8 * (n))) & 0xff)
/* used for keyExpansion */
#define MIX(x) (((S[BYTE(x, 2)] << 24) & 0xff000000) ^ ((S[BYTE(x, 1)] << 16) & 0xff0000) ^ \
((S[BYTE(x, 0)] << 8) & 0xff00) ^ (S[BYTE(x, 3)] & 0xff))
#define ROF32(x, n) (((x) << (n)) | ((x) >> (32-(n))))
#define ROR32(x, n) (((x) >> (n)) | ((x) << (32-(n))))
/* for 128-bit blocks, Rijndael never uses more than 10 rcon values */
static const uint32_t rcon[10] = {
0x01000000UL, 0x02000000UL, 0x04000000UL, 0x08000000UL, 0x10000000UL,
0x20000000UL, 0x40000000UL, 0x80000000UL, 0x1B000000UL, 0x36000000UL
};
unsigned char S[256] = {
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
};
unsigned char inv_S[256] = {
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D
};
/* copy in[16] to state[4][4] */
int loadStateArray(uint8_t(*state)[4], const uint8_t* in) {
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[j][i] = *in++;
}
}
return 0;
}
/* copy state[4][4] to out[16] */
int storeStateArray(uint8_t(*state)[4], uint8_t* out) {
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
*out++ = state[j][i];
}
}
return 0;
}
int keyExpansion(const uint8_t* key, uint32_t keyLen, AesKey* aesKey) {
if (NULL == key || NULL == aesKey) {
printf("keyExpansion param is NULL\n");
return -1;
}
if (keyLen != 16) {
printf("keyExpansion keyLen = %d, Not support.\n", keyLen);
return -1;
}
uint32_t* w = aesKey->eK;
uint32_t* v = aesKey->dK;
/* keyLen is 16 Bytes, generate uint32_t W[44]. */
/* W[0-3] */
for (int i = 0; i < 4; ++i) {
LOAD32H(w[i], key + 4 * i);
}
/* W[4-43] */
for (int i = 0; i < 10; ++i) {
w[4] = w[0] ^ MIX(w[3]) ^ rcon[i];
w[5] = w[1] ^ w[4];
w[6] = w[2] ^ w[5];
w[7] = w[3] ^ w[6];
w += 4;
}
w = aesKey->eK + 44 - 4;
for (int j = 0; j < 11; ++j) {
for (int i = 0; i < 4; ++i) {
v[i] = w[i];
}
w -= 4;
v += 4;
}
return 0;
}
int addRoundKey(uint8_t(*state)[4], const uint32_t* key) {
uint8_t k[4][4];
/* i: row, j: col */
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
k[i][j] = (uint8_t)BYTE(key[j], 3 - i); /* copy uint32 key[4] to uint8 k[4][4] */
state[i][j] ^= k[i][j];
}
}
return 0;
}
int subBytes(uint8_t(*state)[4]) {
/* i: row, j: col */
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[i][j] = S[state[i][j]];
}
}
return 0;
}
int invSubBytes(uint8_t(*state)[4]) {
/* i: row, j: col */
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[i][j] = inv_S[state[i][j]];
}
}
return 0;
}
int shiftRows(uint8_t(*state)[4]) {
uint32_t block[4] = { 0 };
/* i: row */
for (int i = 0; i < 4; ++i) {
LOAD32H(block[i], state[i]);
block[i] = ROF32(block[i], 8 * i);
STORE32H(block[i], state[i]);
}
return 0;
}
int invShiftRows(uint8_t(*state)[4]) {
uint32_t block[4] = { 0 };
/* i: row */
for (int i = 0; i < 4; ++i) {
LOAD32H(block[i], state[i]);
block[i] = ROR32(block[i], 8 * i);
STORE32H(block[i], state[i]);
}
return 0;
}
/* Galois Field (256) Multiplication of two Bytes */
uint8_t GMul(uint8_t u, uint8_t v) {
uint8_t p = 0;
for (int i = 0; i < 8; ++i) {
if (u & 0x01) { //
p ^= v;
}
int flag = (v & 0x80);
v <<= 1;
if (flag) {
v ^= 0x1B; /* x^8 + x^4 + x^3 + x + 1 */
}
u >>= 1;
}
return p;
}
int mixColumns(uint8_t(*state)[4]) {
uint8_t tmp[4][4];
uint8_t M[4][4] = { {0x02, 0x03, 0x01, 0x01},
{0x01, 0x02, 0x03, 0x01},
{0x01, 0x01, 0x02, 0x03},
{0x03, 0x01, 0x01, 0x02} };
/* copy state[4][4] to tmp[4][4] */
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
tmp[i][j] = state[i][j];
}
}
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[i][j] = GMul(M[i][0], tmp[0][j]) ^ GMul(M[i][1], tmp[1][j])
^ GMul(M[i][2], tmp[2][j]) ^ GMul(M[i][3], tmp[3][j]);
}
}
return 0;
}
int invMixColumns(uint8_t(*state)[4]) {
uint8_t tmp[4][4];
uint8_t M[4][4] = { {0x0E, 0x0B, 0x0D, 0x09},
{0x09, 0x0E, 0x0B, 0x0D},
{0x0D, 0x09, 0x0E, 0x0B},
{0x0B, 0x0D, 0x09, 0x0E} };
/* copy state[4][4] to tmp[4][4] */
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
tmp[i][j] = state[i][j];
}
}
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[i][j] = GMul(M[i][0], tmp[0][j]) ^ GMul(M[i][1], tmp[1][j])
^ GMul(M[i][2], tmp[2][j]) ^ GMul(M[i][3], tmp[3][j]);
}
}
return 0;
}
int aesEncrypt(const uint8_t* key, uint32_t keyLen, const uint8_t* pt, uint8_t* ct, uint32_t len) {
AesKey aesKey;
uint8_t* pos = ct;
const uint32_t* rk = aesKey.eK;
uint8_t out[BLOCKSIZE] = { 0 };
uint8_t actualKey[16] = { 0 };
uint8_t state[4][4] = { 0 };
if (NULL == key || NULL == pt || NULL == ct) {
printf("param err.\n");
return -1;
}
if (keyLen > 16) {
printf("keyLen must be 16.\n");
return -1;
}
if (len % BLOCKSIZE) {
printf("inLen is invalid.\n");
return -1;
}
memcpy(actualKey, key, keyLen);
keyExpansion(actualKey, 16, &aesKey);
for (int i = 0; i < len; i += BLOCKSIZE) {
loadStateArray(state, pt);
addRoundKey(state, rk);
for (int j = 1; j < 10; ++j) {
rk += 4;
subBytes(state);
shiftRows(state);
mixColumns(state);
addRoundKey(state, rk);
}
subBytes(state);
shiftRows(state);
addRoundKey(state, rk + 4);
storeStateArray(state, pos);
pos += BLOCKSIZE;
pt += BLOCKSIZE;
rk = aesKey.eK;
}
return 0;
}
int aesDecrypt(const uint8_t* key, uint32_t keyLen, const uint8_t* ct, uint8_t* pt, uint32_t len) {
AesKey aesKey;
uint8_t* pos = pt;
const uint32_t* rk = aesKey.dK;
uint8_t out[BLOCKSIZE] = { 0 };
uint8_t actualKey[16] = { 0 };
uint8_t state[4][4] = { 0 };
if (NULL == key || NULL == ct || NULL == pt) {
printf("param err.\n");
return -1;
}
if (keyLen > 16) {
printf("keyLen must be 16.\n");
return -1;
}
if (len % BLOCKSIZE) {
printf("inLen is invalid.\n");
return -1;
}
memcpy(actualKey, key, keyLen);
keyExpansion(actualKey, 16, &aesKey);
for (int i = 0; i < len; i += BLOCKSIZE) {
loadStateArray(state, ct);
addRoundKey(state, rk);
for (int j = 1; j < 10; ++j) {
rk += 4;
invShiftRows(state);
invSubBytes(state);
addRoundKey(state, rk);
invMixColumns(state);
}
invSubBytes(state);
invShiftRows(state);
addRoundKey(state, rk + 4);
storeStateArray(state, pos);
pos += BLOCKSIZE;
ct += BLOCKSIZE;
rk = aesKey.dK;
}
return 0;
}
int main() {
// case 1
const uint8_t key[16] = { 0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c };
const uint8_t pt[16] = { 0x32, 0x43, 0xf6, 0xa8, 0x88, 0x5a, 0x30, 0x8d, 0x31, 0x31, 0x98, 0xa2, 0xe0, 0x37, 0x07, 0x34 };
uint8_t ct[16] = { 0 };
uint8_t plain[16] = { 0 };
aesEncrypt(key, 16, pt, ct, 16);
printHex(pt, 16, "plain data:");
printf("expect cipher:\n39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32\n");
printHex(ct, 16, "after encryption:");
aesDecrypt(key, 16, ct, plain, 16);
printHex(plain, 16, "after decryption:");
// case 2
const uint8_t key2[] = "1234567890123456";
const uint8_t* data = (uint8_t*)"abcdefghijklmnopqrstuvwxyz123456";
uint8_t ct2[32] = { 0 };
uint8_t plain2[32] = { 0 };
aesEncrypt(key2, 16, data, ct2, 32);
printf("\nplain text:\n%s\n", data);
printf("expect ciphertext:\nfcad715bd73b5cb0488f840f3bad7889\n");
printHex(ct2, 32, "after encryption:");
aesDecrypt(key2, 16, ct2, plain2, 32);
printHex(plain2, 32, "after decryption:");
printf("output plain text\n");
for (int i = 0; i < 32; ++i) {
printf("%c ", plain2[i]);
}
return 0;
}
4.逆向
特征1:
S盒
特征2:
密钥扩展

特征3:
初始轮异或:

特征4:
主循环轮

特征5:
列混淆
5.EX
1.AES支持128、192和256位密钥长度,分别对应10、12和14轮加密。
2.
| 模式 | 是否需要填充 | 并行性支持 | 认证支持 | 典型应用场景 |
|---|---|---|---|---|
| ECB | 是 | 是 | 否 | 单块独立数据(不推荐通用场景) |
| CBC | 是 | 否 | 否 | 文件加密、传统协议(如TLS 1.2) |
| CTR | 否 | 是 | 否 | 实时流数据(视频/音频传输) |
| CFB | 否 | 部分 | 否 | 流式处理(需逐字节加密) |
| OFB | 否 | 否 | 否 | 高容错环境(如卫星通信) |
| GCM | 否 | 是 | 是 | 现代网络协议(TLS 1.3、IPSec) |
| XTS | 否 | 是 | 否 | 磁盘/存储加密(全盘加密) |
1.8 RSA
1.简介
RSA(Rivest-Shamir-Adleman)是最早的非对称加密算法之一,基于大整数分解的数学难题。其核心特点是公钥加密、私钥解密,广泛应用于数据加密、数字签名和密钥协商。
2.算法实现
- 密钥生成
- 选择两个大质数:随机生成两个大质数p和q(通常为1024位以上)。
- 计算模数n:n = p × q。
- 计算欧拉函数φ(n):φ(n) = (p-1)(q-1)。
- 选择公钥指数e:1 < e < φ(n),且e与φ(n)互质(常用e=65537)。
- 计算私钥指数d:d ≡ e⁻¹ mod φ(n)(通过扩展欧几里得算法求逆元)。
- 生成密钥对。
- 加密
- c=me mod n
- 解密
- m=cd mod n
3.代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
// 最大位数限制(仅为示例,实际需要大整数库)
#define MAX_DIGITS 1000
typedef struct {
long long public_exponent; // e
long long private_exponent; // d
long long modulus; // n
} RSA_KeyPair;
// 计算最大公约数(GCD)
long long gcd(long long a, long long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
// 扩展欧几里得算法求模逆元
long long mod_inverse(long long e, long long phi) {
long long d = 0;
long long x1 = 0, x2 = 1, y1 = 1, y2 = 0;
long long q, r, x, y;
long long a = phi;
long long b = e;
while (b != 0) {
q = a / b;
r = a % b;
x = x2 - q * x1;
y = y2 - q * y1;
a = b;
b = r;
x2 = x1;
x1 = x;
y2 = y1;
y1 = y;
}
d = x2 % phi;
if (d < 0) d += phi;
return d;
}
// 快速幂取模运算 (base^exp % mod)
long long mod_pow(long long base, long long exp, long long mod) {
long long result = 1;
base = base % mod;
while (exp > 0) {
if (exp % 2 == 1)
result = (result * base) % mod;
exp = exp >> 1;
base = (base * base) % mod;
}
return result;
}
// 生成 RSA 密钥对(简化版,未使用真实质数生成算法)
RSA_KeyPair generate_rsa_keys() {
RSA_KeyPair key;
long long p = 61; // 示例质数(实际应随机生成大质数)
long long q = 53; // 示例质数
long long n = p * q;
long long phi = (p - 1) * (q - 1);
long long e = 17; // 选择与 phi 互质的指数
// 计算私钥 d
long long d = mod_inverse(e, phi);
key.public_exponent = e;
key.private_exponent = d;
key.modulus = n;
return key;
}
// 加密函数
long long rsa_encrypt(long long plaintext, long long e, long long n) {
return mod_pow(plaintext, e, n);
}
// 解密函数
long long rsa_decrypt(long long ciphertext, long long d, long long n) {
return mod_pow(ciphertext, d, n);
}
int main() {
// 生成密钥对
RSA_KeyPair key = generate_rsa_keys();
printf("Public Key (e, n): (%lld, %lld)\n", key.public_exponent, key.modulus);
printf("Private Key (d, n): (%lld, %lld)\n", key.private_exponent, key.modulus);
// 加密示例
long long plaintext = 42; // 明文必须小于 n
long long ciphertext = rsa_encrypt(plaintext, key.public_exponent, key.modulus);
printf("Encrypted: %lld\n", ciphertext);
// 解密示例
long long decrypted = rsa_decrypt(ciphertext, key.private_exponent, key.modulus);
printf("Decrypted: %lld\n", decrypted);
return 0;
}
0xFF EX
1.1 各类算法初始常量
对于使用默认算法的程序可以从初始常量直接判断使用了哪个算法,因此记录一下个算法的初始常量。
- md5
- 初始向量:
| 寄存器 | 十六进制值 | 十进制值 |
|---|---|---|
| A | 0x67452301 | 1732584193 |
| B | 0xEFCDAB89 | -271733879 |
| C | 0x98BADCFE | -1732584194 |
| D | 0x10325476 | 271733878 |
- 常量表:
| i | T[i] (十六进制) | T[i] (十进制) |
|---|---|---|
| 1 | 0xd76aa478 | 3614090360 |
| 2 | 0xe8c7b756 | 3905402710 |
| 3 | 0x242070db | 606105819 |
| 4 | 0xc1bdceee | 3250441966 |
| 5 | 0xf57c0faf | 4118548399 |
| 6 | 0x4787c62a | 1200080426 |
| 7 | 0xa8304613 | 2821735955 |
| 8 | 0xfd469501 | 4249261313 |
| 9 | 0x698098d8 | 1770035416 |
| 10 | 0x8b44f7af | 2336552879 |
| 11 | 0xffff5bb1 | 4294925233 |
| 12 | 0x895cd7be | 2304563134 |
| 13 | 0x6b901122 | 1804603682 |
| 14 | 0xfd987193 | 4254626195 |
| 15 | 0xa679438e | 2792965006 |
| 16 | 0x49b40821 | 1236535329 |
| 17 | 0xf61e2562 | 4129170786 |
| 18 | 0xc040b340 | 3225465664 |
| 19 | 0x265e5a51 | 643717713 |
| 20 | 0xe9b6c7aa | 3921069994 |
| 21 | 0xd62f105d | 3593408605 |
| 22 | 0x02441453 | 38016083 |
| 23 | 0xd8a1e681 | 3634488961 |
| 24 | 0xe7d3fbc8 | 3889429448 |
| 25 | 0x21e1cde6 | 568446438 |
| 26 | 0xc33707d6 | 3275163606 |
| 27 | 0xf4d50d87 | 4107603335 |
| 28 | 0x455a14ed | 1163531501 |
| 29 | 0xa9e3e905 | 2850285829 |
| 30 | 0xfcefa3f8 | 4243563512 |
| 31 | 0x676f02d9 | 1735328473 |
| 32 | 0x8d2a4c8a | 2368359562 |
| 33 | 0xfffa3942 | 4294588738 |
| 34 | 0x8771f681 | 2272392833 |
| 35 | 0x6d9d6122 | 1839030562 |
| 36 | 0xfde5380c | 4259657740 |
| 37 | 0xa4beea44 | 2763975236 |
| 38 | 0x4bdecfa9 | 1272893353 |
| 39 | 0xf6bb4b60 | 4139469664 |
| 40 | 0xbebfbc70 | 3220217754 |
| 41 | 0x289b7ec6 | 681279174 |
| 42 | 0xeaa127fa | 3936430074 |
| 43 | 0xd4ef3085 | 3572445317 |
| 44 | 0x04881d05 | 76029189 |
| 45 | 0xd9d4d039 | 3654602809 |
| 46 | 0xe6db99e5 | 3873151461 |
| 47 | 0x1fa27cf8 | 530742520 |
| 48 | 0xc4ac5665 | 3299628645 |
| 49 | 0xf4292244 | 4096336452 |
| 50 | 0x432aff97 | 1126891415 |
| 51 | 0xab9423a7 | 2878612391 |
| 52 | 0xfc93a039 | 4237533241 |
| 53 | 0x655b59c3 | 1700485571 |
| 54 | 0x8f0ccc92 | 2399980690 |
| 55 | 0xffeff47d | 4293915773 |
| 56 | 0x85845dd1 | 2240044497 |
| 57 | 0x6fa87e4f | 1873313359 |
| 58 | 0xfe2ce6e0 | 4264355552 |
| 59 | 0xa3014314 | 2734768916 |
| 60 | 0x4e0811a1 | 1309151649 |
| 61 | 0xf7537e82 | 4149444226 |
| 62 | 0xbd3af235 | 3174756917 |
| 63 | 0x2ad7d2bb | 718787259 |
| 64 | 0xeb86d391 | 3951481745 |
- SHA-1
- 初始向量:
| 寄存器 | 十六进制值 | 十进制值 |
|---|---|---|
| H0 | 0x67452301 | 1732584193 |
| H1 | 0xEFCDAB89 | -271733879 |
| H2 | 0x98BADCFE | -1732584194 |
| H3 | 0x10325476 | 271733878 |
| H4 | 0xC3D2E1F0 | -1009589776 |
- K表:
| 轮次 | t 取值范围 | K 值(十六进制) | K 值(十进制) |
|---|---|---|---|
| 轮 1 | 0 ≤ t ≤ 19 | 0x5A827999 | 1518500249 |
| 轮 2 | 20 ≤ t ≤ 39 | 0x6ED9EBA1 | 1859775393 |
| 轮 3 | 40 ≤ t ≤ 59 | 0x8F1BBCDC | -1894007588 |
| 轮 4 | 60 ≤ t ≤ 79 | 0xCA62C1D6 | -899497514 |
- SHA-256
- 初始向量:
| 寄存器 | 十六进制值 | 十进制值 |
|---|---|---|
| H0 | 0x6A09E667 | 1779033703 |
| H1 | 0xBB67AE85 | 3144134277 |
| H2 | 0x3C6EF372 | 1013904242 |
| H3 | 0xA54FF53A | 2773480762 |
| H4 | 0x510E527F | 1359893119 |
| H5 | 0x9B05688C | 2600822924 |
| H6 | 0x1F83D9AB | 528734635 |
| H7 | 0x5BE0CD19 | 1541459225 |
- K表:
| i | K[i] (十六进制) | K[i] (十进制) |
|---|---|---|
| 0 | 0x428A2F98 | 1116352408 |
| 1 | 0x71374491 | 1899447441 |
| 2 | 0xB5C0FBCF | 3049323471 |
| 3 | 0xE9B5DBA5 | 3921009573 |
| 4 | 0x3956C25B | 961987163 |
| 5 | 0x59F111F1 | 1508970993 |
| 6 | 0x923F82A4 | 2453635748 |
| 7 | 0xAB1C5ED5 | 2870763221 |
| 8 | 0xD807AA98 | 3624381080 |
| 9 | 0x12835B01 | 310598401 |
| 10 | 0x243185BE | 607225278 |
| 11 | 0x550C7DC3 | 1426881987 |
| 12 | 0x72BE5D74 | 1925078388 |
| 13 | 0x80DEB1FE | 2162078206 |
| 14 | 0x9BDC06A7 | 2614888103 |
| 15 | 0xC19BF174 | 3248222580 |
| 16 | 0xE49B69C1 | 3835390401 |
| 17 | 0xEFBE4786 | 4022224774 |
| 18 | 0x0FC19DC6 | 264347078 |
| 19 | 0x240CA1CC | 604807628 |
| 20 | 0x2DE92C6F | 770255983 |
| 21 | 0x4A7484AA | 1249150122 |
| 22 | 0x5CB0A9DC | 1555081692 |
| 23 | 0x76F988DA | 1996064986 |
| 24 | 0x983E5152 | 2554220882 |
| 25 | 0xA831C66D | 2821834349 |
| 26 | 0xB00327C8 | 2952996808 |
| 27 | 0xBF597FC7 | 3210313671 |
| 28 | 0xC6E00BF3 | 3336571891 |
| 29 | 0xD5A79147 | 3584528711 |
| 30 | 0x06CA6351 | 660778143 |
| 31 | 0x14292967 | 764128156 |
| 32 | 0x27B70A85 | 956783617 |
| 33 | 0x2E1B2138 | 1012266030 |
| 34 | 0x4D2C6DFC | 1188179964 |
| 35 | 0x53380D13 | 1322822218 |
| 36 | 0x650A7354 | 1537002063 |
| 37 | 0x766A0ABB | 1747873779 |
| 38 | 0x81C2C92E | 1955562222 |
| 39 | 0x92722C85 | 2024104815 |
| 40 | 0xA2BFE8A1 | 2227730452 |
| 41 | 0xA81A664B | 2361852424 |
| 42 | 0xC24B8B70 | 2428436474 |
| 43 | 0xC76C51A3 | 2756734187 |
| 44 | 0xD192E819 | 3204031479 |
| 45 | 0xD6990624 | 3329325298 |
| 46 | 0xF40E3585 | 3614090360 |
| 47 | 0x106AA070 | 4096336452 |
| 48 | 0x19A4C116 | 275423344 |
| 49 | 0x1E376C08 | 430227734 |
| 50 | 0x2748774C | 506948616 |
| 51 | 0x34B0BCB5 | 659060556 |
| 52 | 0x391C0CB3 | 883997877 |
| 53 | 0x4ED8AA4A | 958139571 |
| 54 | 0x5B9CCA4F | 1322822218 |
| 55 | 0x682E6FF3 | 1537002063 |
| 56 | 0x748F82EE | 1747873779 |
| 57 | 0x78A5636F | 1955562222 |
| 58 | 0x84C87814 | 2024104815 |
| 59 | 0x8CC70208 | 2227730452 |
| 60 | 0x90BEFFFA | 2361852424 |
| 61 | 0xA4506CEB | 2428436474 |
| 62 | 0xBEF9A3F7 | 2756734187 |
| 63 | 0xC67178F2 | 3204031479 |
- SHA-512
- 初始向量:
| 寄存器 | 十六进制值 | 十进制值 |
|---|---|---|
| H0 | 0x6A09E667F3BCC908 | 7640891576956012808 |
| H1 | 0xBB67AE8584CAA73B | 13503953896175478587 |
| H2 | 0x3C6EF372FE94F82B | 9141506630228921602 |
| H3 | 0xA54FF53A5F1D36F1 | 8127029997194072455 |
| H4 | 0x510E527FADE682D1 | 1067661582809310611 |
| H5 | 0x9B05688C2B3E6C1F | 15266992153038912541 |
| H6 | 0x1F83D9ABFB41BD6B | 7310566010038615275 |
| H7 | 0x5BE0CD19137E2179 | 12641808001770024935 |
- K表(80 轮):
| i | K[i] (十六进制) | K[i] (十进制) |
|---|---|---|
| 0 | 0x428A2F98D728AE22 | 4794697086780616226 |
| 1 | 0x7137449123EF65CD | 8158064640168781261 |
| 2 | 0xB5C0FBCFEC4D3B2F | 13096744586834688815 |
| 3 | 0xE9B5DBA58189DBBC | 16840607885511220156 |
| 4 | 0x3956C25BF348B538 | 4131703408338449720 |
| 5 | 0x59F111F1B605D019 | 6480981068601479193 |
| 6 | 0x923F82A4AF194F9B | 10841863296015460430 |
| 7 | 0xAB1C5ED5DA6D8118 | 11840083180663258601 |
| 8 | 0xD807AA98A3030242 | 13761210420658862357 |
| 9 | 0x12835B0145706FBE | 1955562227530015923 |
| 10 | 0x243185BE4EE4B28C | 2566078912744131131 |
| 11 | 0x550C7DC3D5FFB4E2 | 5820280999292360768 |
| 12 | 0x72BE5D74F27B896F | 7000572520888010196 |
| 13 | 0x80DEB1FE3B1696B1 | 8329554718502883634 |
| 14 | 0x9BDC06A725C71235 | 9653372634249731737 |
| 15 | 0xC19BF174CF692694 | 12306992647733299338 |
| 16 | 0xE49B69C19EF14AD2 | 14659517364153108720 |
| 17 | 0xEFBE4786384F25E3 | 15287077618968449919 |
| 18 | 0x0FC19DC68B8CD5B5 | 2003953874473911977 |
| 19 | 0x240CA1CC77AC9C65 | 2754233442935904083 |
| 20 | 0x2DE92C6F592B0275 | 3202212388942662810 |
| 21 | 0x4A7484AA6EA6E483 | 4219281265443770937 |
| 22 | 0x5CB0A9DCBD41FBD4 | 4897197038893956785 |
| 23 | 0x76F988DA831153B5 | 5936983446876343111 |
| 24 | 0x983E5152EE66DFAB | 7416221891901391085 |
| 25 | 0xA831C66D2DB43210 | 8333317564501964585 |
| 26 | 0xB00327C898FB213F | 9921213316382820384 |
| 27 | 0xBF597FC7BEEF0EE4 | 10499252185670484601 |
| 28 | 0xC6E00BF33DA88FC2 | 11112610896997822385 |
| 29 | 0xD5A79147930AA725 | 12128233816726201911 |
| 30 | 0x06CA6351E003826F | 1328613116552530738 |
| 31 | 0x142929670A0E6E70 | 1435262141778498825 |
5.blowfish
P-box
| 索引 | 值 (十六进制) | 索引 | 值 (十六进制) |
|---|---|---|---|
| 0 | 0x243F6A88 | 9 | 0x38D01377 |
| 1 | 0x85A308D3 | 10 | 0xBE5466CF |
| 2 | 0x13198A2E | 11 | 0x34E90C6C |
| 3 | 0x03707344 | 12 | 0xC0AC29B7 |
| 4 | 0xA4093822 | 13 | 0xC97C50DD |
| 5 | 0x299F31D0 | 14 | 0x3F84D5B5 |
| 6 | 0x082EFA98 | 15 | 0xB5470917 |
| 7 | 0xEC4E6C89 | 16 | 0x9216D5D9 |
| 8 | 0x452821E6 | 17 | 0x8979FB1B |
S-box
S-box 0(部分示例)
| 索引 | 值 (十六进制) | 索引 | 值 (十六进制) |
|---|---|---|---|
| 0 | 0xD1310BA6 | 4 | 0xB8E1AFED |
| 1 | 0x98DFB5AC | 5 | 0x6A267E96 |
| 2 | 0x2FFD72DB | 6 | 0xBA7C9045 |
| 3 | 0xD01ADFB7 | ... | ... |
S-box 1(部分示例)
| 索引 | 值 (十六进制) | 索引 | 值 (十六进制) |
|---|---|---|---|
| 0 | 0x4B7A70E9 | 4 | 0xAD6EA6B0 |
| 1 | 0xB5B32944 | 5 | 0x49A7DF7D |
| 2 | 0xDB75092E | 6 | 0x9CEE60B8 |
| 3 | 0xC4192623 | ... | ... |
1.2 参考网址
1.美国国家标准与技术研究院(NIST, National Institute of Standards and Technology) 的官方出版物网站。它提供 NIST 发布的各类技术文档、标准、指南和研究论文,涵盖 网络安全、密码学、人工智能、物理测量、量子计算 等多个领域。https://nvlpubs.nist.gov/
2.openssl:https://github.com/openssl/openssl/blob/master/crypto/bf/bf_pi.h
文章评论